eExploring The Different Types Of Probability!

Probability is a fundamental concept in mathematics and statistics that quantifies the likelihood of an event occurring. It is a crucial tool for analyzing uncertainty and making informed decisions in various fields such as science, engineering, finance, and everyday life. There are several types of probability, each with its own interpretation and application.

Firstly, classical probability, also known as theoretical probability, is  on equally likely outcomes and is often in situations with known and finite sample spaces.

Secondly, empirical probability, or experimental probability, is derive from observe frequencies of events occurring in repeate experiments or real-world data.

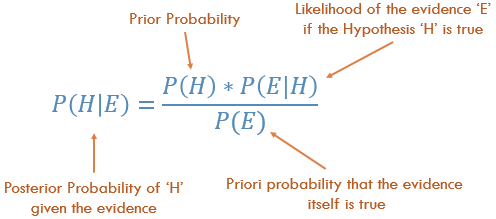
Finally, conditional probability measures the likelihood of an event occurring given that another event has already occurred, and is essential for modeling dependencies and making predictions in uncertain environments.

Probability Density Function (PDF)

The Probability Density Function (PDF): a function for continuous data whose value at any point can be interpreted as indicating the probability that the random variable's value will equal that sample.

Probability Mass Function (PMF):  a discrete data function that calculates the likelihood of a given value occurring.

Cumulative Density Function (CDF): The integral of the CDF is a function that tells us the probability that a random variable is less than a certain value.

Uniform Distribution: a probability distribution where all outcomes are equally likely.