Outliers in Machine Learning

Outliers in Machine Learning, Are you the one who is looking forward to knowing Outlier detection introduction in Machine Learning? Or the one who is looking forward to knowing outlier detection techniques in Machine Learning and the effects of outliers in data or Are you dreaming to become to certified Pro Machine Learning Engineer or Data Scientist, then stop just dreaming, get your Data Science certification course with Machine Learning from India’s Leading Data Science training institute.

Outliers are data points that are distant from other similar points due to variability in the measurement. Outliers should be excluded from the data set but detecting of those outliers is very difficult which is not always possible. The below blog clearly explains your effects of outliers in data and how to identify outliers in data. Do you want to know outlier detection introduction, So follow the below-mentioned outliers in the machine learning tutorial from Prwatech and take advanced Data Science training with Machine Learning like a pro from today itself under 10+ Years of hands-on experienced Professionals.

Outlier Detection Introduction

A data point that lies outside the overall distribution of the dataset is called an outlier of the data. An outlier is an observation point that is distant from other observations statistically, i.e. Outlier is separate or different from a point or set of points in the group. So in short we can call it as ‘odd man out’ from the dataset

Effects of Outliers in data:

Due to variability in data or experimental errors like mistakes in data collection, recording, and entry, the datasets contain outliers. In the case of statistical analysis, it can cause major problems like :

Data skewing

Errors in the mean of the data set.

Errors in the standard deviation of the data set.

How to Identify Outliers in Data?

To identify these outliers we have to take two approaches in the frame.

We have to find those data points which fall outside of 1.5 times an interquartile range above the 3rd quartile and below the 1st quartile.

We have to find data points that fall outside of 3 standard deviations. We can use a z score also.

Different Types of Outliers:

In different datasets, we have to deal specifically with two types of outliers.

Uni variate (one variable outlier), where single variable outlier analysis is done.

Multivariate outliers (Two or more variable outliers), If we have one categorical value, then with that we can check multiple continuous variables.

How to Handle Outliers in Data?

Finding outliers with visualization tools

Using scatter plots:

A scatter plot is a sort of mathematical illustration used to display values for typically two variables for a set of data. It uses Cartesian coordinates. The data are displayed as a collection of points, in which each point having the value of one variable determines the position on the horizontal axis and the other variable determines the position on the vertical axis.

First load the Boston file from sklearn.

import pandas as pd

import numpy as np

from sklearn.datasets import load_boston

boston = load_boston()

x = boston.data

y = boston.target

columns = boston.feature_names

#create the data frame with x and y

df = pd.DataFrame(boston.data)

df.columns = columns

df.head()

To check the scatter plot, we can access variables named ‘INDUS’ and ‘TAX’ from Boston data.

import matplotlib.pyplot as plt

%matplotlib inline

fig, testplot = plt.subplots(figsize=(16,8))

testplot.scatter(df[‘INDUS’], df[‘TAX’])

testplot.set_xlabel(‘Proportion of non-retail business acres per town’)

testplot.set_ylabel(‘Full-value property-tax rate’)

plt.show()

It will give a graphical view as,

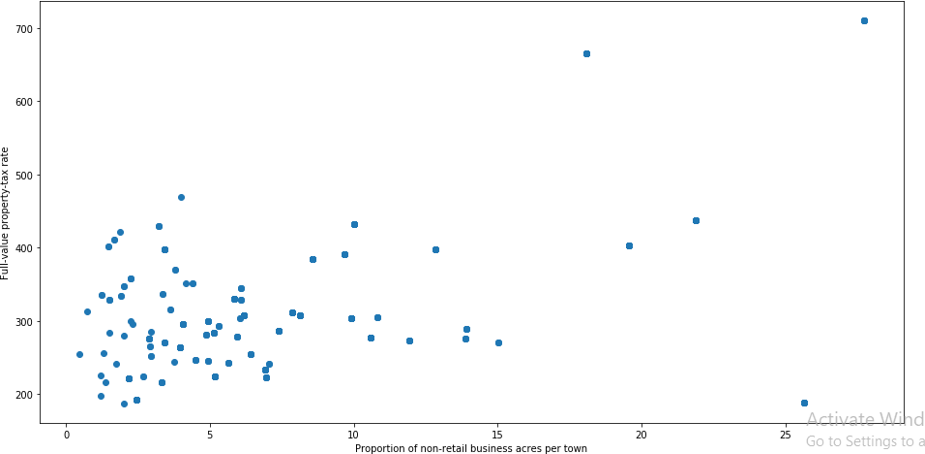
From the above plot, it is observed clearly that the points having the same features are collectively placed at the left bottom and points which are outliers are placed far away from the group.

Using Box Plots:

A box plot is a method for representing collections of numerical data through their quartiles. Outliers may be plotted as individual points in this graphical representation. So from this, we can find out the separately placed points in the box plot as outliers.

First load the boston file from sklearn:

import pandas as pd

import numpy as np

from sklearn.datasets import load_boston

boston = load_boston()

x = boston.data

y = boston.target

columns = boston.feature_names

#create the data frame with x and y

df = pd.DataFrame(boston.data)

df.columns = columns

df.head()

Now we will plot the box plot using ‘box plot’

import seaborn as sns

sns.boxplot(x=df[‘DIS’])

We get the box plot as:

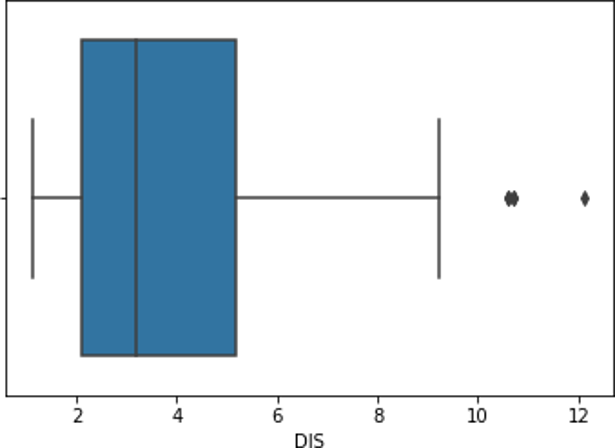
As shown in the box plot the points which are outliers are placed or plotted separate points. The univariate outlier is analyzed here as a single variable column called ‘DIS’ is only taken into account to check the outlier. But we can do multivariate outlier analysis also in case of any categorical value. Here continuous variables can be analyzed with any categorical value.

Finding Outliers with Mathematical Function

Using Z-score:

Z-score is used to describe any data point by finding their relationship with the Standard Deviation of the dataset and the Mean of the group of data points. Z-score is identifying the normal distribution of data where the mean is 0 and the standard deviation is 1.

from scipy import stats

import numpy as np

z = np.abs(stats.zscore(data))
print(z)

threshold=3

print(np.where(z>3))

Correcting and removing the outliers using z-score:

data = data[(z < 3).all(axis=1)]

Using Interquartile range (IQR):

The interquartile range (IQR) is a quantity to measure of dispersion, like standard deviation or variance, based on the division of a data set into quartiles. The data set is divided into four equal parts. The values that divide each part are known as the first, second, and third quartiles; and they are denoted by Q1, Q2, and Q3, respectively.

Q1 is the central value in the first half of the data set.

Q2 is the median value in the dataset.

Q3 is the central value in the second half of the data set.

The interquartile range is nothing but the difference between Q3 and Q1. We will find outliers in the same data using IQR.

Q1 = df.quantile(0.25)

Q3 = df.quantile(0.75)

IQR = Q3 – Q1

print(IQR)

It will show the result of having a list that contains IQR for each row. Now to find out the outliers we can write.

print(df < (Q1 – 1.5 * IQR)) |(df > (Q3 + 1.5 * IQR))

The result will give output in form of True or False values. True means the values which fall after and before the third and first quartile. These values are outliers in the dataset, which can be removed as:

df_clean = df[~((df< (Q1 – 1.5 * IQR)) |(df > (Q3 + 1.5 * IQR))).any(axis=1)]

df_clean will give the dataset excluding outliers.

We hope you understand outliers in Machine Learning concepts and outlier detection techniques, how to handle outliers in data. Get success in your career as a Data Scientist/ Machine Learning Engineer by being a part of the Prwatech, India’s leading Data Science training institute in Bangalore.