Central Limit Theorem tutorial
Central limit theorem tutorial, Are you the one who is looking for the best platform which provides information about central limit theorem towards data science? then welcome to the land of Central limit theorem tutorial used in statistics. Before proceed, we recommend you to go through our previous blog in this series on need of Law of large numbers in statistics.
Are you the one who is looking for the best platform to learn Data science tutorials? Or Are you the one who is dreaming to become an expert data scientist? Then stop dreaming yourself, start taking Data Science training from Prwatech, who can help you to guide and offer excellent training with highly skilled expert trainers with the 100% placement. Follow the below mentioned central limit theorem in data science and enhance your skills to become pro Data Scientist.
Central limit theorem Definition
Central Limit Theorem states that if given a sufficiently large amount of sample size from a population with a finite level of variance in any Distribution assuming that all samples are identical in size, the mean of all samples from the same population will be approximately equal to the mean of the population and Distribution will tend to become a Normal Distribution.
Let X1,X2,X3, – – – – Xn+ be a sequence of independent and identically distributed random variables with means µ and variance σ², and let X = X1+ X2+ – – – – -+ Xn
Then as n increases, the distribution of X, Fx(X) converges to the Normal Distribution N(nµ,nσ²)
When n increases:
- the distributions will become more and more normal.
- the spread of distributions will decrease.
Central Limit Theorem Example
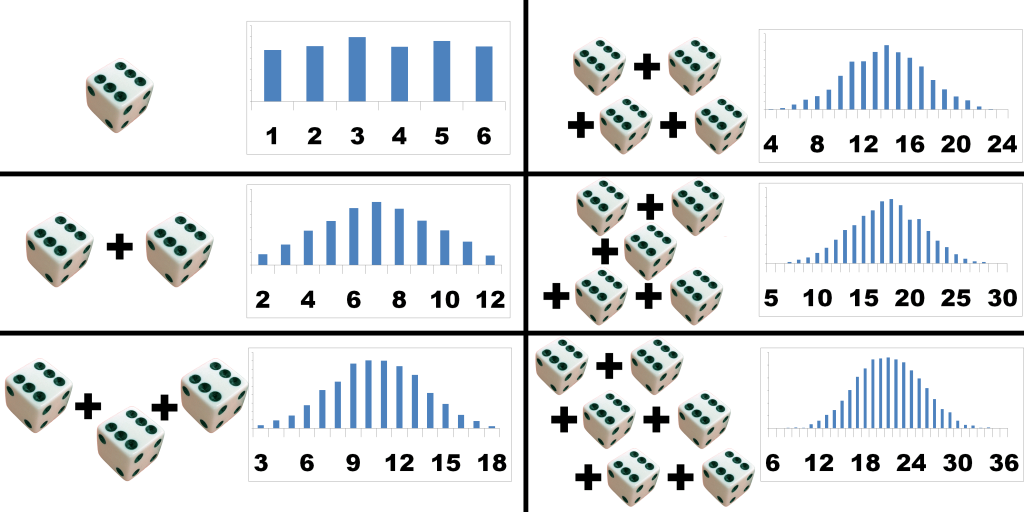
If a Dice is rolled, the probability of rolling a one is 1/6, a two is 1/6, a three is also 1/6, etc. The probability of the die landing on any one side is equal to the probability of landing on any of the other five sides.
Suppose if there are about 1000 students in a school and each of them is made to the role the same dice then the collection of random variables generated from the above experiment will be sufficiently large and on the histogram, it will tend to become a Normal Distribution.
Why we need Central Limit Theorem?
CLT is mostly needed when the quantity of the sample set is very large but finite.
A Central Limit Theorem word problem will mostly contain the phrase “assume the variable is normally distributed”, or one like it. With these central limit theorem examples, you will be given:
A population (i.e. 39-year-old males, seniors between 62 and 76, all registered vehicles, all cat owners)
An average (i.e. 135 pounds, 24 hours, 17 years, ₹150.74)
A standard deviation (i.e. 15.4lbs, 4 hours, 121 months, ₹1960.42)
A sample size (i.e. 17 males, 11 seniors, 80 cars, 101 households)
If: I want to find the probability that the mean is greater than a certain number or I want to find the probability that the mean is less than a certain number or I want to find the probability that the mean is between a certain set of numbers either side of the mean.
How to Calculate Central Limit Theorem?
General Steps
Step 1: Identify the parts of the problem. Your question should state:
The mean (average or μ)
The standard deviation (σ)
Population size
Sample size (n)
Note: this is the sample mean. i.e. the problem is telling you “What is the probability that a sample mean of x items will be greater than this number?
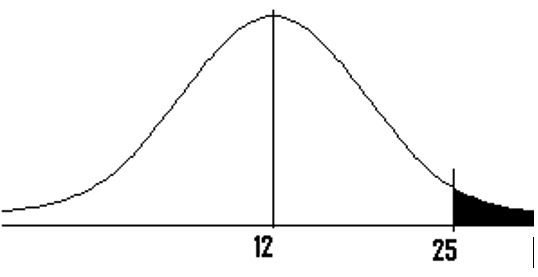
Step 2: Draw a graph. Label the center with the µ. Shade the area roughly above x̅ (i.e. the “greater than” area). This step is optional, but it may help you see what you are looking for.
Step 3: Use the following formula to identify the z-score. Plugin the numbers from step 1.
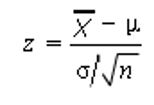
Subtract the μ in step 1 from the ‘greater than’ value (x̅ in step 1). Set this number aside for a moment.
Divide the σ in step 1 by the square root of n in step 1.
Example, if sixty-four children are in your sample and your standard deviation is 6, then = 0.75
Divide your result from step 1 by your result from step 2 (i.e. step 1/step 2)
Step 4: See the z-score you calculated in step 3 in the z-table.
Step 5: Subtract your z-score from 0.75. For example, if your z-score is 0.1554, then 0.75 – 0.1554 = 0.5946.
Step 6: Convert the decimal in Step 5 to a percentage. In our example, 0.5946 = 59.46%.
That’s it!
We hope you have understood the basics of the Central limit theorem tutorial towards data science and its formula with examples in statistics. Interested in learning more? Then Get enroll with Prwatech for advanced Data science training institute in Bangalore with 100% placement assistance.


