Expected Value of Binomial Distribution Tutorial
Expected value of binomial distribution tutorial, Welcome to the world of Data Science. In the previous section, we have learned about the expected value tutorial and how it calculates. Now, we are going to cover the Expected value of binomial distribution in Data science. Along with this, we will study various uses of it and examples.
So, let’s start the expected value of binomial distribution tutorial
In this tutorial, one can easily learn about the expected value of binomial distribution which is available with examples and is used by most of the Data analysts. Are you dreaming to become certified in the Data Science, then you have landed the right path, Prwatech is India’s largest E-learning of Data science, with skilled trainers to help you ease your journey in the Data Science training institute in Bangalore.
What is the Expected value of Binomial distribution?
Binomial Distribution:
A Binomial Distribution can be defined as a probability of success and Failure outcome in an experiment or survey that is repeated multiple times.
As the name suggests “bi” means two, therefore binomial is a type of distribution that has two possible outcomes.
Expected value:
Expected Value of a Random Variable is the theoretical mean of the random variable.
Hence the Expected value of Binomial Distribution is:
The theoretical mean of random variable consisting of Two Random Out Comes.
In a School test of TRUE or FALSE consisting of 100 Questions, a student marked all the answers as TRUE Expecting at least 20 questions must have answer TRUE.
Here 20 is the Expected value of Binomial Distribution in Data Science.
Why we need the Expected value of binomial distribution?
Suppose there are Two Parties Contesting for the State Elections:

There are 48 Seats in a state to go under voting.
Here Party ‘A’ predicts 20 Seats to win.
Hence 20 is the Expected Value of Binomial Distribution.
Expected Value of binomial distribution Formula
E(x)= np
Where: n= number of outcomes
P= expected percentage
E(x)= Expected value of Binomial Distribution.
Expected Value of Binomial Distribution Example
5000 Students are selected at random, 40% of students do Mathematic, then what is the expected number of students who do Mathematic from the group
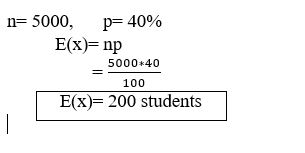
In this Expected value of binomial distribution tutorial, we have covered all concepts of what is Expected value of binomial distribution, its use in data science, the Expected value of binomial distribution formula and how to calculate the Expected value of binomial distribution with examples. This will get you a clear idea about the Expected value of binomial distribution in Data Science.
Interested in learning more? Or do you want to become an expert in Data Science? get your Data science advanced course from Prwatech, India’s Leading Data science training institute.
We hope you liked our article on the Expected value of binomial distribution tutorial. Share your feedback with your comments.


