Two-Tailed Test Tutorial

Two-tailed test tutorial, Welcome to the world of a two-tailed test in Data science using python. Now, we are going to cover the introduction of the two-tailed test tutorial. Along with this, we will study various uses of it and formula to calculate with example.

Thinking of having a career as a Data analyst? Planning to go for a certification in Data science and related subjects but still not getting a conviction whether it is the right thing to do or not? Confused about whether to invest time in gaining knowledge of Data science or not? Such questions can give you sleepless nights, but by taking an advanced data science course from India’s largest E-Learning data science training institute in Bangalore, I am sure that you will get a lot of reasons to build a data science career.

Two-tailed test Definition

A test of a statistical hypothesis, where the area of rejection is on both sides of the sampling distribution, is known as the Two-Tailed Test.

As the name suggests Two Tail Test is a test involving a lower part or the part at the Tails on both sides of the curve is known as the Two-Tailed Test.

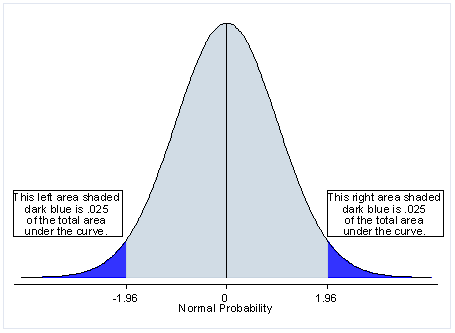
Over a Normal Distribution bell-shaped cure, two tail test divides the value of rejection into two equivalent parts of the same size at the end of the curve.

At 5 % of rejection in a two-tail test, each part of rejection is 2.5 % such that standard deviation is less then -1.96 and more than 1.96, and 95% of Acceptance.

Why we use a two-tail test?

To test the Null Hypothesis or non-directional hypothesis. i.e. there is no significant difference between the null hypothesis.

It is used when positive or negative direction value is not possible.
Where: Ho: M1-M2 =0.

Ho: M1=M2

To find any difference or not between two means.

Suppose the null hypothesis states that the mean is equal to 70. The alternative hypothesis will be that the mean is less than 70 or greater than 70. The region of rejection will include a range of numbers located on both sides of sampling distribution; i.e. the region of rejection will include parts of numbers that were less than 70 and partly of numbers that were greater than 70.

How to use Two Tail Test?

As a hypothetical example, imagine a situation that a new stockbroker (DLF) claims that his brokerage fees are lower than that of your current stock broker’s (ABC). Data available from an independent research firm specifies that the mean and standard deviation of all ABC broker clients are $22 and $9, respectively.

A sample of 600 clients of ABC are chosen and brokerage charges are calculated with the new rates of DLF broker. If the mean of the sample is $15 and the sample standard deviation is $9, can any inference be made about the difference in the average brokerage bill between ABC and DLF broker?

H0 = 15

H1<> 15(This is what we want to prove.)

Rejection region: Z <= – Z 2.5 and Z>=Z 2.5 (assuming 5% significance level, split 2.5 each on either side).

 Two-tailed Test Example

This calculated Z value falls between the two limits defined by: – Z2.5 = -1.96 and Z2.5 = 1.96.

This concludes that there is insufficient evidence to infer that there is any difference between the rates of your existing broker and the new broker. Alternatively, the p-value = P(Z< -1.25)+P(Z >1.25) = 2 * 0.1056 = 0.2112 = 21.12%, which is greater than 0.05 or 5%, leads to the same conclusion.

H0 = 15

H1<> 18

Rejection region: Z <= – Z2.5 and Z>=Z2.5 (assuming 5% significance level, split 2.5 each on either side).

Z = (sample mean – mean) / (std-dev / sqrt (no. of samples))

=(18.75 – 18) / (6/()

= 1.25

This calculated Z value falls between the two limits defined by: – Z2.5 = -1.96 and Z2.5 = 1.96.

This indicates that there is insufficient evidence to conclude that there is any difference between the rates of your existing broker and the new broker. Alternatively, the p-value = P (Z< -1.25) + P (Z >1.25) = 2 * 0.1056 = 0.2112 = 21.12%, which is greater than 0.05 or 5%, leads to the same conclusion.

We hope you have understood the basics of the two-tailed test tutorial with examples in data science. Be a part of future technologies like Data Science. Register from Data Science Training in Bangalore by industry experts at Prwatech.