Type 1 error and Type 2 error tutorial

Type 1 error and Type 2 error tutorial, hunting for the best platform which provides information about Type 1 error and Type 2 error in statistics? Then welcome to the land of Type 1 error and Type 2 error tutorial in Data Science. In this tutorial, one can explore what is Type 1 error and Type 2 error, examples of Type 1 error and Type 2 error and the importance of Type 1 error and Type 2 error in data science which were prepared by India’s leading Data Science training institute professionals.

Thinking of having a career as a Data analyst? Planning to go for a certification in Data science and related subjects but still not getting a conviction whether it is the right thing to do or not? Confused about whether to invest time in gaining knowledge of Data science or not? Such questions can give you sleepless nights, but by taking an advanced data science course from India’s largest E-Learning data science training institute in Bangalore, I am sure you will get a lot of reasons to build a data science career.

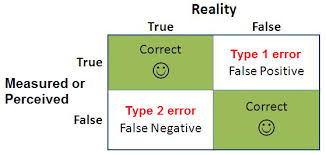
Type 1 error definition

A type 1 error is a type of error that occurs during a hypothesis testing process when a null hypothesis is rejected even though it is true and should not be rejected. In hypothesis testing, a null hypothesis is established before starting a test. In some cases, the null hypothesis assumes the absence of a cause and effect relationship between the items being tested and the inducement being applied to the test subject in pursuance of triggering an outcome to the test.

This is denoted as “n=0”.

Why we use a Type 1 error in statistics?

Sometimes, rejecting a null hypothesis that there is no relationship between the test subject, the inducement and the outcome can be incorrect. If the result of the test is caused by something other than the inducement, it can cause a “false positive” outcome where it appears the inducement acted upon the subject, but the outcome was actually caused by chance. This “false positive,” leading to an incorrect rejection of the null hypothesis, is called a type I error. A type I error rejects an idea that must not have been rejected.

Example of a Type 1 Error

Let’s consider the trail of an accused criminal.

The alternate hypothesis is that the person is guilty, while the Null Hypothesis is innocent.

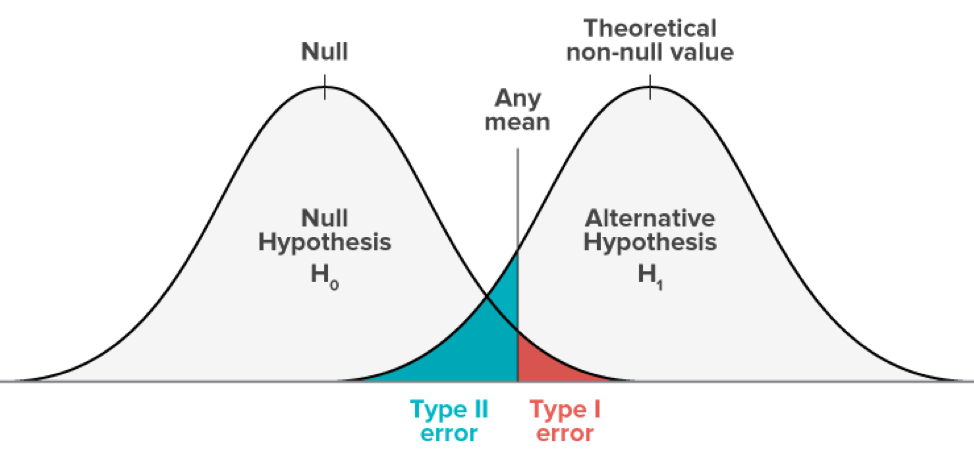
Type 2 error definition

In other words, it produces a false positive. The error rejects the alternative hypothesis, even after it does not occur due to chance.

Why we need a Type 2 error in statistics?

Consider a biotechnology organization that wants to compare how effective two of its drugs are for treating cancer.

The null hypothesis states the two medicines are equally effective.

A null hypothesis (Ho), claims that the organization hopes to reject using the one-tailed test.

The alternative hypothesis (Hα), states that two drugs are not equally effective. The alternative hypothesis, Hα, is the measurement supported by rejecting the null hypothesis.

Example of a Type 2 Error

The biotech organization implements a large clinical trial of 9,000 patients with cancer to compare the treatments. The company expects, two drugs must have an equal number of patients to determine that both drugs are effective.

Assume beta is calculated to be 2.5%. Hence, the probability of committing a type 2 error is 2.5%. If the two medications are not equally effective, the null hypothesis should be rejected. However, if the biotech organization does not reject the null hypothesis when the drugs are not equally effective, a type 2 error occurs. We hope you have understood the basics of the Type 1 error and Type 2 error tutorial and its formula with examples in data science. Planning towards becoming a skilled expert in Data Science? If so, be a part of the Prwatech learning program of Data Science Training in Bangalore.